binary tree

Problem

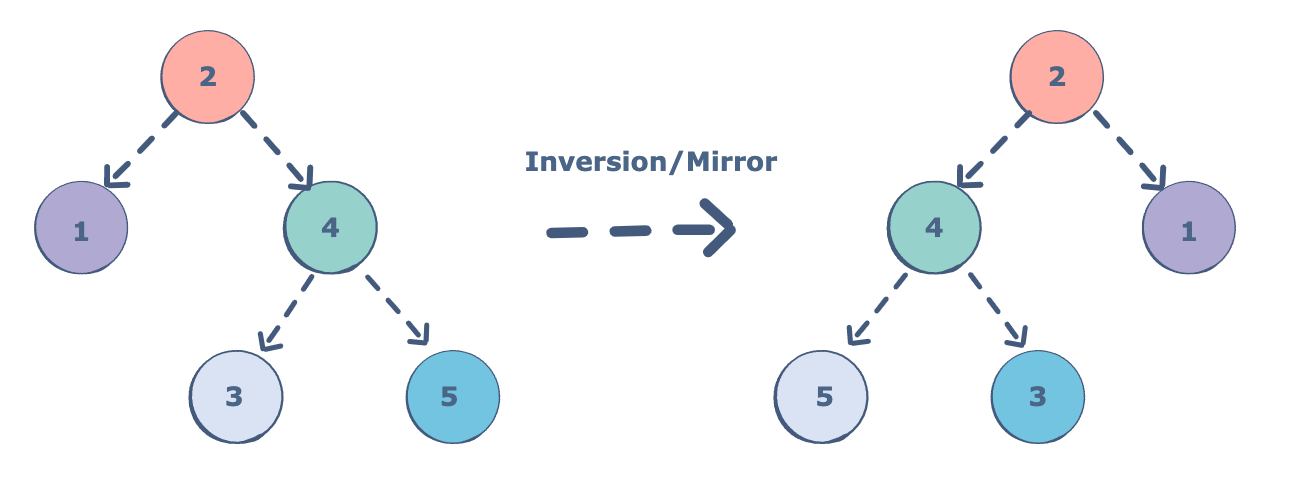
Binary tree is a data structure and one of the simplest form of trees. You might have heard about people complaining [1] that during interviews they are asked to invert a binary tree. It may sound like something difficult, but in this article I’ll show you really simple solution using recursion (see this article for more recursion in Python). Inverting a tree basically means to switch places for right and left children of each node. Resulting tree will look like vertical mirroring of the input. Therefore if you know how to represent a tree within a code, you won’t stuck adding just a couple of extra lines invoking recursive function.

NOTE: Python 3.10 is used throughout the article.

Data structures

First of all we need a data structure which represents a tree and two helper functions:
generate_tree to create a target tree we plan to work with and
print_tree to visualize the result and verify our solution works as intended.

To represent a tree we need to define only one class that corresponds to a node. Each node stores some value/identificator as well as pointers to its children or None in case of leaf nodes. An arbitrary variable assigned to the root node will state as a tree within our code.

1
2
3
4
5
6
7
8
9
10
11
class Node(object):
    def __init__(self, value: int = None):
        self.value = value
        self.left: Node = None
        self.right: Node = None

    def __str__(self):
        return f'{self.value}'

    def __repr__(self) -> str:
        return self.__str__()

Having this class defined we can go ahead and compose some simple tree by creating couple of linked nodes.

1
2
3
4
5
6
left_leaf = Node(23)
right_leaf = Node(42)
root = Node(0)
root.left = left_leaf
root.right = right_leaf
tree = root  # this is our simple tree consisting of three nodes total

Storing one variable (root node) is enough to represent a whole tree as the rest of nodes are linked together using pointers.

Creating a tree manually is a hassle, so we need a function that generates arbitrary tree for us. We will provide number of levels as an argument and it will return a root node for the tree requested. Each node stores sequentually incremented value for better visual grasp, but you can also fill the tree with some random numbers.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from typing import Optional

counter = 0

def generate_tree(levels: int) -> Optional[Node]:
    global counter
    if levels == 0:
        return None

    counter += 1
    node = Node(counter)
    node.left = generate_tree(levels-1)
    node.right = generate_tree(levels-1)
    return node

We leverage recursion to generate left and right subtrees until we reach leaf nodes therefore returning None for their children. To check whether generation was any good we need to add print_tree function which is going to output its target to the console.

1
2
3
4
5
6
7
def print_tree(node: Node, level: int = 0):
    if node is None:
        return
    print_tree(node.right, level+1)
    print('  ' * level, end='')
    print(node)
    print_tree(node.left, level+1)

Again, idea is to use recursion for traversing left and right subtrees and putting each node’s value to the terminal in between. level parameter allows to add an extra indentation, so it’s visually clear on which level the node resides. Finally, we have a tree representation which looks like tree laying on its side (rotated counter-clockwise)

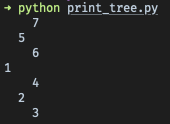
print tree

1
2
tree = generate_tree(3)
print_tree(tree)

Use lines above if you want to produce same output as on the screenshot.

Recursive solution

It’s no surprise that for inverting our tree we are going to use recursion again. This simple and straightforward solution requires even less code than generation itself.

1
2
3
4
5
6
7
8
9
10
def invert_tree(node: Node) -> Node:
    if node is None:
        return

    left_inverted = invert_tree(node.left)
    right_inverted = invert_tree(node.right)
    # Switch places for left and right
    node.right = left_inverted
    node.left = right_inverted
    return node

The algorithm is the following: strarting from the root we invoke this function for the left and right subtrees and then swap them with each other. Therefore we end up having symmetrical tree from the same root node.

1
2
3
4
5
6
7
tree = generate_tree(3)
print('Initial tree')
print_tree(tree)
inverted = invert_tree(tree)
print('-'*5)
print_tree(inverted)
print('Inverted tree')

inverted tree

As you can see the resulting tree is symmetrical along the horizontal axis, so when folded on the dashed line corresponding nodes will match.

That’s basically it for the inversion itself. Clearly, there are more of extra code to help us represent and visualize the solution than within the solution itself. It gets tricky though when we want to accomplish the same without any recursion. Let’s move on to see how the same can be done using queue.

Non-recursive solution

NOTE: There is also a slightly simpler solution using stack data structure. We are not going to implement it within the article as internally recursive solution works by storing all the function invocations on the stack. Basically that solution is equivalent of maintaining own call stack and essentially follows the exact same principle. Anyway, you can find source code for the stack-based solution within resources section in the end of the article.

The algorithm consists of two main steps: on the first stage we use breadth first search to traverse the tree and on the way we add leaf nodes to the intermediate list; on the second stage we restore tree-like structure from list elements rearraged in the desired order. Let’s look at each stage in more detail.

First stage

This is a simple implementation of a BFS that converts our input tree to the linear array of nodes.

1
2
3
4
5
6
7
8
9
10
11
12
def flatten_tree(node: Node) -> List[Node]:
    flatten = []
    queue = [node]
    while queue:
        node = queue.pop()
        if node:
            flatten.append(node)
            # Add order doesn't matter, but
            # it needs to be inverted on the second stage
            queue.insert(0, node.right)
            queue.insert(0, node.left)
    return flatten

The output of the function is a list containing all the elements in a specific order. This allows us to rebuild a tree attaching leaf nodes differently thus achieving requested order.

Second stage

To understand better what this step does consider we are working with [1, 5, 2, 7, 6, 4, 3] list as an input. You can obtain this exact order by going over our example tree from left to right column by column. Then based on the current position (counter) we look ahead and mount leaf nodes back to the current node in the queue. flatten/expand stages complement each other, so we should re-mount in the order opposite to the previous step. As a result left and right leaves for the each node got swapped.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def expand_into_tree(elems: List[Node]) -> Node:
    queue = []
    counter = 0
    root = Node(elems[counter])
    queue.append(root)
    while queue:
        node = queue.pop()
        # Note the inversed order here
        if left := _get(elems, counter+1):
            node.left = left
            queue.insert(0, left)
            counter += 1

        if right := _get(elems, counter+1):
            node.right = right
            queue.insert(0, right)
            counter += 1

    return root

There is also a helper _get function simply to make getitem operation safe for our code. It makes sure no IndexError occurs when we reach the end of our list and there is no more nodes to attach.

1
2
3
4
5
6
7
8
9
from typing import List, Optional, TypeVar

T = TypeVar('T')

def _get(array: List[T], index: int) -> Optional[T]:
    try:
        return array[index]
    except IndexError:
        pass

Code is a simple wrapper with try/catch block returning None when the index is out of bounds.

That’s everything we need to invert our tree non-recursively:

1
2
3
def invert_tree_queue(root: Node) -> Node:
    linear_elems = flatten_tree(root)
    return expand_into_tree(linear_elems)

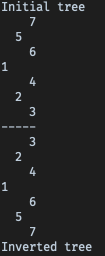
Finally, confirm the solution works properly and matches previous results:

1
2
3
tree = generate_tree(3)
inverted = invert_tree_queue(tree)
print_tree(inverted)

NOTE: Solution above works only with balanced trees where each non-leaf node has two children. This restriction comes up from the relying on the explicit order or the elements in the flattened tree. As an excersise you can modify the code to make it more general.

Final words

I don’t necessarily think that knowing all the algorithms and ability to write them on the whiteboard is a required thing for the programmer to have. As long as your code does something useful or cover some business need your are valuable for the field. Nowadays, especially with tools like GitHub Copilot and DeepMind AlphaCode you can write sophisticated code only by providing description of the feature required. Nevertheless, understanding main ideas and underlying concepts would hugely help you during development/debugging process. You don’t have to implement everything yourself or follow instructions step-by-step, but at least try to keep these articles as a side-reading. Stay curious, see ya.

Resources