Невеличка стаття на примітивно-базовому рівні про те, як працюють регулярні вирази. Я хотів би написати серію про створення власного транслятора і це може бути одним із таких постів. Тут я опишу коротку програму, яка буде перевіряти вхідний рядок на відповідність нашому заданому регулярному виразу.

Регулярний вираз - це граматика, що задає мову. Простіше кажучи, це група правил, записаних у вигляді набору символів, що визначає, якого вигляду конструкції може містити певна задана мова.

Щоб написати програму, що буде розбирати регулярний вираз, потрібно розуміти поняття автомату.

Автомат - це сутність, що визначається такими поняттями:

M = (Q, T, q0, d, F)

Q - множина всіх станів автомата.

T - множина вхідних символів.

q0 - початковий стан (входить в множину Q).

d - функція переходів автомата.

F - множина кінцевих станів автомата (підмножина Q).

Побудуємо автомат, що буде розбирати регулярний вираз E = (+ | - | e) d d*.

E (expression) - регулярний вираз.

e (empty) - порожній рядок.

d (digit) - цифра.

| (вертикальна риска, pipe) - операція або. Повинен бути присутній хоча б один символ з перелічених.

* - символ може повторюватися довільну кількість разів (від нуля до нескінченності).

Потрібно виділити всі можливі стани і відповідні переходи до них. Найпростіше це подати графічно:

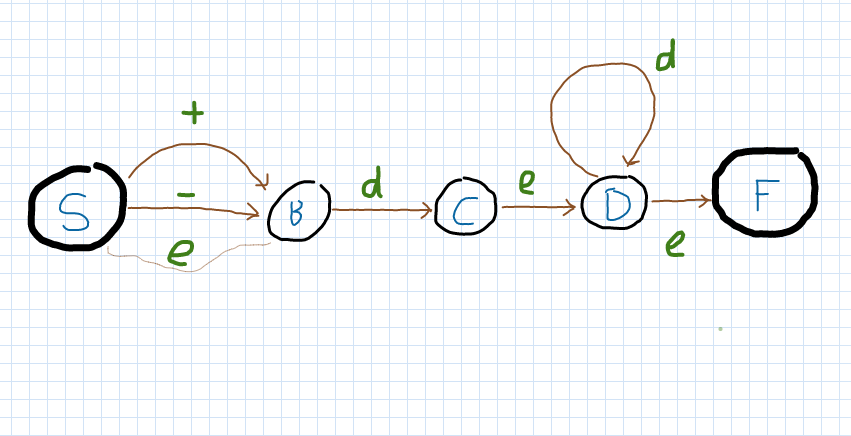
states

S (start) - це початковий стан, F (finish) - кінцевий. З початкового стану ми можемо прочитати символи додавання, віднімання чи нічого (порожній символ) і перейти в стан B зчитування цифри. В стані C у нас уже є гарантовано одна цифра і ми переходимо безумовно (по порожньому символу) в стан D. В ньому ми можемо крутитися в циклі доти, доки зустрічаємо цифру або ж одразу перейти в кінцевий стан F. Тепер ми знаємо всі можливі умови і переходи, які можна записати кодом:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class InvalidInput(ValueError):
    pass


def match_string(text):

    def read_char():
        yield from text

    cursor = read_char()
    try:
        ch = next(cursor)

        if ch == '+' or ch == '-':
            ch = next(cursor)

        if ch.isdigit():
            while True:
                try:
                    ch = next(cursor)
                except StopIteration:
                    break
                if not ch.isdigit():
                    raise InvalidInput('Number should contain only digits')

        else:
            raise InvalidInput('Number should start with a digit')

    except StopIteration:
        raise InvalidInput('Unexpected end of input')

Все що тут відбувається - це посимвольне зчитування вхідних даних і перевірка на відповідність поточного символа очікуваному стану. Якщо символ не відповідає стану - отримаємо помилку вхідних даних InvalidInput. Даною програмою тепер можна перевіряти рядки на відповідність нашому регулярному виразу. Так всередині влаштовані багато інструментів розбору регулярок.

Але коли регулярка стає складнішою, а вхідний текст довшим - хочеться мати змогу швидко знайти місце помилки в разі невірних вхідних даних. Таку функціональність ми спробуємо додати до нашого аналізатору.

Створимо клас

1
2
3
4
class Matcher(object):
    def __init__(self, text):
        self.pos = 0
        self.text = text

що буде зберігати позицію останнього зчитаного символу. Також додамо два методи для отримання наступного символу і відображення помилки

1
2
3
4
5
6
7
8
9
10
11
12
def read(self):
    for pos, char in enumerate(self.text):
        self.pos = pos
        yield char

def error(self, message):
    term.writeLine('Error at position {pos}: {message}'.format(
        pos=self.pos, message=message), term.red)
    term.writeLine(self.text)
    term.write('-'*self.pos, term.yellow)
    term.write('^\n', term.yellow)
    raise InvalidInput(message)

І сам метод match майже без модифікацій

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def match(self):
    cursor = self.read()
    try:
        ch = next(cursor)

        if ch == '+' or ch == '-':
            ch = next(cursor)

        if ch.isdigit():
            while True:
                try:
                    ch = next(cursor)
                except StopIteration:
                    break
                if not ch.isdigit():
                    self.error('Number should contain only digits')

        else:
            self.error('Number should start with a digit')

    except StopIteration:
        self.error('Unexpected end of input')

Тепер коли виникне помилка - ми побачимо інформативне повідомлення з вказанням місця в рядку, де вона була виявлена.

error

Ресурси