Привіт, зараз дуже популярними є напрямки штучного інтелекту, нейронних мереж та машинного навчання. Все це побудовано на досить нескладних концептах, які можна відтворити, знаючи трохи математики та програмування. Саме це ми і зробимо сьогодні, використовуючи Python 3.

Для початку потрібно розуміти, що собою буде являти нейронна мережа. Будемо думати про неї, як про функцію, що отримує деякий набір вхідних даних та видає для них результат. Ззовні це виглядає як чорний ящик, внутрішню будову якого ми будемо розглядати. Отож, наше завдання - використовуючи набір вхідних даних навчити нашу нейронну мережу, щоб вона максимально точно відображала зв’язок вхідних та вихідних даних. Потрібно знайти найкращу апроксимацію функції відображення вхідних даних у вихідні.

Вхідні дані

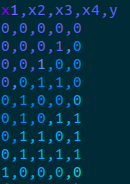
Щоб перевірити коректність роботи нашої мережі, ми будемо використовувати деяку зазделегідь відому нам функцію, яку ми використаємо для генерації вхідних даних, а також поведінку якої ми будемо намагатися повторити в процесі навчання. Отже, функція буде приймати 4 вхідних параметри x1, x2, x3, x4 та повертати результат y, що рівний виразу (x1 and x2) or (x3 and x4). Область визначення та область значень функції - множина з двох елементів {0, 1}

1
2
3
def f(X):
    x1, x2, x3, x4 = X
    return (x1 or x2) and (x3 or x4)

Залишилось перебрати всі можливі комбінації і порахувати результат, що ми будемо використовувати як еталонний.

1
2
3
4
5
6
7
8
9
10
11
12
from itertools import product
import pandas as pd

def main():
    columns = ['x1', 'x2', 'x3', 'x4', 'y']
    data = []
    for elem in product([0, 1], repeat=4):
        row = [*elem, f(elem)]
        data.append(row)

    df = pd.DataFrame(data, columns=columns)
    df.to_csv('data.csv', header=True, index=False)

Тут і далі в коді використовується бібліотека для роботи з даними pandas (взагалі, для конкретного прикладу можна обійтися і без неї, але вона є стандартом при обробці вхідних даних, тому буде корисно познайомитися зі зразком її використання). Також для операції з матрицями та векторами будемо використовувати бібліотеку numpy. В результаті отримаємо файл з таким вмістом head data.csv

dataset

Трохи теорії

Нейронні мережі складаються з таких основних компонентів: вхідні дані (X(x1, x2, ..., xn)), вихідні дані (y), один або декілька прихованих шарів, набір коефіцієнтів між кожним з шарів (W(w1, w2, ..., wn)) та функцій активації для кожного прихованого шару.
Для нашого випадку найпростіша мережа буде виглядати так

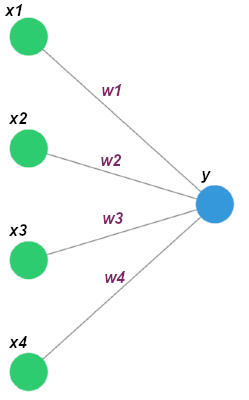
network 1

Якщо з вхідними даними, шарами та коефіцієнтами все досить просто (це звичайний вектор/матриця), то розглянути функцію активації потрібно трохи детальніше. Вона визначає залежність вхідного сигналу від вихідного (найпростішим для розуміння варіантом є тотожна функція, яка просто повертає вхідний параметр f(x) = x). Але в нейронних мережах найчастіше використовується сигмоїда, тому ми теж скористаємося нею у нашому прикладі.

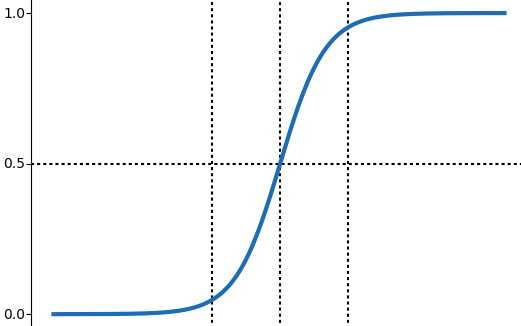
sigmoid

Формула для функції та відповідне представлення в коді наведено нижче

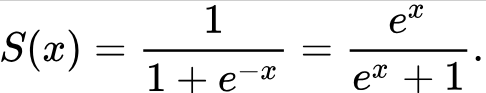
sigmoid equation

1
2
3
4
import numpy as np

def sigmoid(x):
    return 1.0 / (1 + np.exp(-x))

Результатом роботи цієї нейронної мережі є [звичайний добуток] (https://uk.wikipedia.org/wiki/%D0%A1%D0%BA%D0%B0%D0%BB%D1%8F%D1%80%D0%BD%D0%B8%D0%B9_%D0%B4%D0%BE%D0%B1%D1%83%D1%82%D0%BE%D0%BA) вхідного вектора, вектора коефіцієнтів (ваги) та функції активації (сигмоїда).

1
2
3
4
X = np.array([0, 1, 0, 1])
weights = np.array([0, 1, 1, 1])
print(sigmoid(np.dot(X, weights)))
# 0.8807970779778823

Для даного вхідного значення результат близький до очікуваного (1), але для [0, 0, 0, 1] дає досить неточний результат 0.731. Тому далі ми опишемо логіку для коригування коефіцієнтів та використання оновлених значень на кожному наступному кроці. Зміна значень векторів (матриць) коефіцієнтів з кожною ітерацією для знаходження оптимального результату і є процесом навчання нейронної мережі

Будуємо мережу

Наша мережа буде мати один прихований шар і кожна вершина буде поєднана з кожною у наступному шарі. Взагалі є дуже багато топологій нейронних мереж, тому якщо використовувати точну термінологію - ми будемо створювати feed forward мережу(мережа прямого поширення). В початковому прикладі був використаний простий перцептрон. Схематично це виглядає так

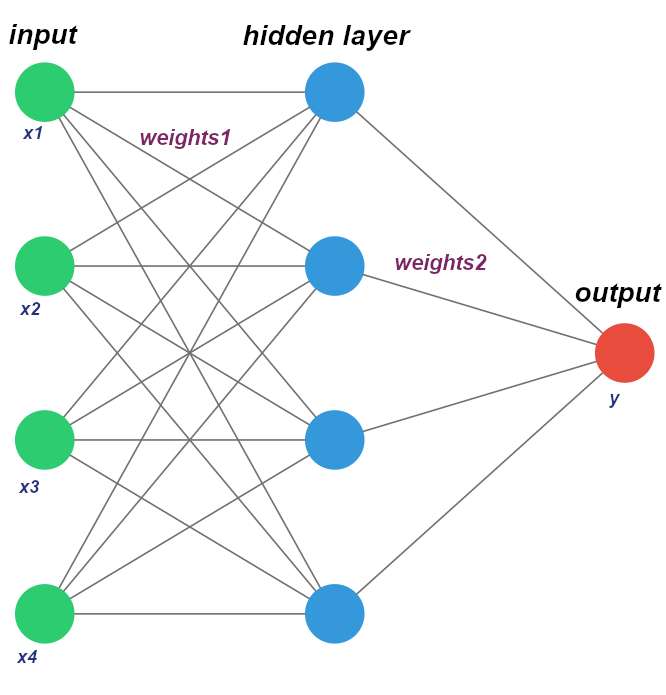
network 2

Тепер додамо функцію для поширення вхідних даних, яка просто почергово перемножає шари на їх коефіцієнти (для простоти ми відкидаємо поправку шару)

1
2
3
def _feed_forward(self):
    self.layer1 = sigmoid(np.dot(self.input, self.weights1))
    self.output = sigmoid(np.dot(self.layer1, self.weights2))

І найскладніша частина мережі - функція зворотнього поширення помилки. Суть полягає в коригуванні значень наших коефіцієнтів

1
2
self.weights1 += d_weights1
self.weights2 += d_weights2

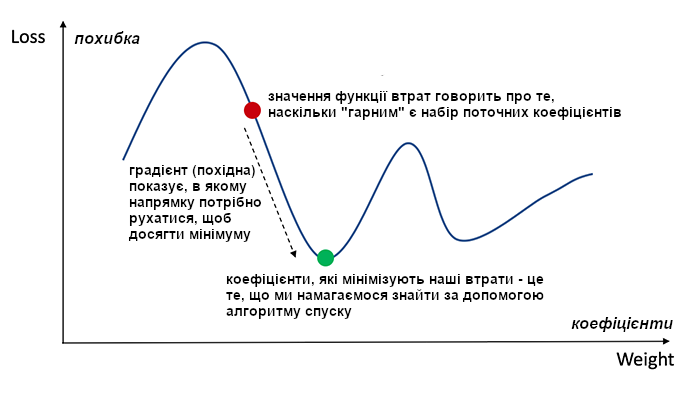
А щоб знайти значення, на які потрібно відкоригувати (змістити) початкові коефіцієнти використовується алгоритм градієнтного спуску. На цьому етапі також вводиться поняття функції втрат - на скільки отримані дані далекі від очікуваних. На кожному кроці ми обчислюємо функцію втрат (loss function), а потім поширюємо цю похибку до попередніх шарів (звідси і назва методу зворотнього поширення помилки). І за допомогою алгоритму градієнтного спуску намагаємося мінімізувати цю похибку.

gradient descent

Для простоти використовуємо в якості функції втрат суму квадратів різниць

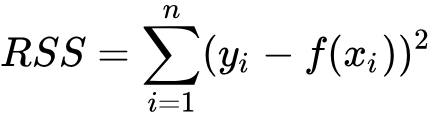
residual sum of squares

Застосовуючи правило диференціювання складеної функції ми можемо знайти похідну функції втрат, враховуючи наші коефіцієнти

Поширення помилки в коді буде виглядати так

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def _back_prop(self):
    loss_derivative_value = 2 * (self.y - self.output)

    sigmoid_derivative_value = sigmoid_derivative(self.output)

    loss_1 = loss_derivative_value * sigmoid_derivative_value
    d_weights2 = np.dot(self.layer1.T, loss_1)

    loss_2 = np.dot(loss_1, self.weights2.T) * \
             sigmoid_derivative(self.layer1)
    d_weights1 = np.dot(self.input.T, loss_2)

    self.weights1 += d_weights1
    self.weights2 += d_weights2

Все, нейронна мережа готова, можемо почати її перевірку в роботі.

Тренуємо мережу

Спочатку отримаємо наші вхідні дані з файлу та поділимо їх на дві частини: дані для тренування мережі та дані для перевірки точності її роботи.

1
2
3
4
5
6
7
8
9
df = pd.read_csv('data.csv')
size = int(len(df)*0.8)
df_train = df[:size]
df_test = df[size:]
X_train = df_train[['x1', 'x2', 'x3', 'x4']].copy()
y_train = df_train.filter(['y'], axis=1)

X_test = df_test[['x1', 'x2', 'x3', 'x4']].copy()
y_test = df_test.filter(['y'], axis=1)

80% вхідних даних використаємо для навчання, а решту для перевірки її роботи. Додамо ще один метод , який буде повторювати процес прямого поширення та зворотнього поширення помилки задану кількість разів (ітерацій).

1
2
3
4
5
6
def fit(self):
    iterations = 1000
    print('Training network...')
    for _ in range(iterations):
        self._feed_forward()
        self._back_prop()

Залишилося лише ініціалізувати мережу та запустити процес навчання

1
2
3
4
5
nn = NeuralNetwork(X_train, y_train)
nn.fit()

with np.printoptions(precision=3, suppress=True):
    print(nn.output)

Тепер наша мережа натренована і ми можемо використовувати її на нових невідомих раніше їй даних (які відповідають формату вхідних даних). Для цього викорстаємо метод predict

1
2
3
4
def predict(self, x):
    layer1 = sigmoid(np.dot(x, self.weights1))
    output = sigmoid(np.dot(layer1, self.weights2))
    return output

Він використовує уже знайдені оптимальні значення коефіцієнтів для обрахування очікуваного результату. Використаємо наш тестовий набір даних для перевірки результатів роботи. Для цього виведемо обраховане значення мережею та дійсне значення для цих вхідних даних.

1
2
for (row, actual) in zip(X_test.values, y_test.values):
    print(nn.predict(row), actual)

Очевидно, що отримані дані дуже близькі до реальних і якби ми ще додали функцію активації на зразок двійкового кроку, то передбачені дані повністю б відповідали фактичним.

1
2
3
4
[0.04475214] [0]
[0.99837902] [1]
[0.99836759] [1]
[0.99979784] [1]

Точність результатів

Отримана мережа показала гарний результат, але як впевнитися в точності її роботи? Яким кількісним показником визначити, наскільки добре вона передбачає результати для нових вхідних даних. Найпростіший спосіб - порахувати кількість правильно передбачених величин і поділити його не довжину всього тестового набору даних. Точність є одним із показників, що використовується у матриці помилок, яка дозволяє всесторонньо оцінити коректність роботи нейронної мережі. Взагалі існує велика кількість метрик, що дозволяють в числовому вигляді відобразити точність мережі під час роботи з раніше невідомими даними. Зауважу, що ми можемо використати як метрику і нашу початкову функцію втрат. Але додатково розглянемо ще одну, RMSE. Вона показує, наскільки близькими в середньому є елементи двох векторів (числа у першому та у другому масиві). Менший показник означає близькі значення обох масивів та менше значення завжди краще. За домогою методу нижче ми порахуємо дану метрику для нашої мережі

1
2
3
4
def accuracy(self, X_test, y_test):
    """RMSE accuracy, lower is better"""
    predictions = self.predict(X_test)
    return np.sqrt(((predictions - y_test) ** 2).mean())

На цьому етапі нам знову знадобляться наші тестові дані

1
2
print('Accuracy (RMSE): {:.4}'.format(nn.accuracy(X_test, y_test)['y']))
# Accuracy (RMSE): 0.02241

Метрики потрібні, щоб порівнювати різні типи мереж чи покращення, які ви вносите в існуючу мережу, щоб переконатися, що зміни дійсно дають кращі результати.

Що далі?

Ми створили просту нейронну мережу, яка змогла досить точно відтворити поведінку оригінальної функції та познайомилися з базовими концептами нейронних мереж. В наступній частині ми за допомогою бібліотеки Keras побудуємо нейронну мережу, яка буде самостійно проходити примітивну гру. Також ознайомимося з методами для отимізації мереж, які дозволять зробити її результати кращими, ніж результати гравця-людини. На цьому все, до зустрічі!

Ресурси