Привіт, сьогодні ми розглянемо модифікацію задачі оптимізації для знаходження найкоротшого (найдешевшого) шляху. Умова така: маємо кубик, на кожній стороні якого позначено додатнє число.

кубик

Коли куб знаходиться на цій стороні - це число додається до загальної вартості шляху. Також маємо площину, поділену на рівні частини (квадрати), які відповідають розміру граней куба. Кубик може переміщуватися по цій площині в чотирьох напрямках (вперед, назад, вправо, вліво) і рух відбувається поворотом у відповідних напрямках відносно осі, яка відповідає ребрам нижньої грані для кожного з напрямків. Простими словами, кубик “перекочується” з однієї грані на іншу, в цей момент ми додаємо до загального шляху “вартість” цієї грані.

Отож, потрібно знайти найдешевший маршрут з точки старту на цій площині до точки фінішу.

Почнемо з представлення даного кубика в коді (будемо використовувати Python 3.7 для прикладів коду). Це просто об’єкт, який зберігає значення вартості для кожної з граней.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Cube(object):
    def __init__(
        self,
        front: int,
        back: int,
        bottom: int,
        top: int,
        left: int,
        right: int
    ):
        self.front = front
        self.back = back
        self.bottom = bottom
        self.top = top
        self.left = left
        self.right = right

    @property
    def value(self):
        return self.bottom

Тепер визначимо методи для руху кубика у всіх чотирьох напрямках, які будуть повертати новий екземляр після кожного такого кроку.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def move_right(self):
    cls = self.__class__
    return cls(
        front=self.front,
        back=self.back,
        bottom=self.right,
        top=self.left,
        left=self.bottom,
        right=self.top,
    )

def move_left(self):
    cls = self.__class__
    return cls(
        front=self.front,
        back=self.back,
        bottom=self.left,
        top=self.right,
        left=self.top,
        right=self.bottom,
    )

def move_forward(self):
    cls = self.__class__
    return cls(
        front=self.bottom,
        back=self.top,
        bottom=self.back,
        top=self.front,
        left=self.left,
        right=self.right,
    )

def move_backward(self):
    cls = self.__class__
    return cls(
        front=self.top,
        back=self.bottom,
        bottom=self.front,
        top=self.back,
        left=self.left,
        right=self.right,
    )

Нічого особливого, але потрібно бути уважним під час зміни граней, щоб кожна опинилася на відповідному місці. Для представлення куба будемо використовувати одну з 11 можливих розгорток.

варіанти розгортки куба

1
2
3
4
5
6
7
8
9
10
11
12
13
def __str__(self):
    space = ' '
    return (
        '{:^3}{:^3}\n'
        '{:^3}{:^3}\n'
        '{:^3}{:^3}{:^3}\n'
        '{:^3}{:^3}\n'
    ).format(
        space, self.top,
        space, self.back,
        self.left, self.bottom, self.right,
        space, self.front,
    )

Тут ми використовуємо синтаксис форматування рядків для кращої наочності. Створимо екземляр, що буде відповідати звичайному гральному кубику і подивимося на результат виводу в консоль.

1
2
3
4
5
6
7
8
9
cube = Cube(
    front=1,
    back=6,
    bottom=5,
    top=2,
    left=3,
    right=4,
)
print(cube)

В результаті маємо таку розгортку:

розгортка в консолі

Перейдемо до представлення грального поля: найпростіший варіант - це двовимірний масив, кожен елемент якого відповідає клітинці поля. Цей підхід затратний по пам’яті, оскільки нам потрібно зберігати клітинки поля, які можуть взагалі не використовуватися впродовж виконання програми. Знаходити шлях для початку будемо найочевиднішим способом за допомогою алгоритму пошуку в ширину. Спочатку ми пробуємо перемістити кубик в усі 4 можливі напрямки.

Кожен з нових положень кубиків ми додаємо в чергу. На карті позначаємо вартість цього шляху: це вартість шляху з попереднього положення + значення грані, на яку ми перемістилися. На кожному наступному кроці ми повторюємо ту ж саму процедуру для кожного елементу в черзі, але записуємо вартість шляху в клітинку поля тільки якщо дана клітинка ще не відвідана раніше, або якщо вартість поточного шляху менша за уже існуючу. Повторюємо це доки не досягли фінішної точки і доки залишилися елементи в нашій черзі.

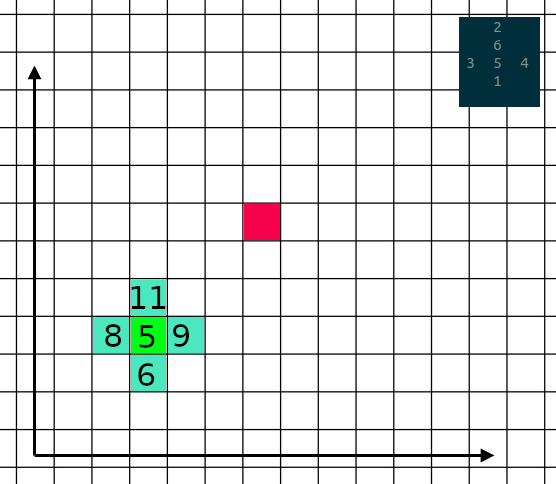
початкова позиція

Черга буде містити пари вигляду (позиція, стан кубика), тож перейдемо до представлення поля і позиції. Для позиції ми використовуємо пару координат на полі

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Position(object):
    def __init__(self, x: int, y: int):
        self.x = x
        self.y = y

    def forward(self):
        cls = self.__class__
        return cls(x=self.x, y=self.y+1)

    def backward(self):
        cls = self.__class__
        return cls(x=self.x, y=self.y-1)

    def left(self):
        cls = self.__class__
        return cls(x=self.x-1, y=self.y)

    def right(self):
        cls = self.__class__
        return cls(x=self.x+1, y=self.y)

    def __eq__(self, other):
        return self.x == other.x and self.y == other.y

    def __str__(self):
        return f'({self.x}, {self.y})'

    def __repr__(self):
        return self.__str__()

    def __hash__(self):
        return hash((self.x, self.y))

Для кожної позиції теж є чотири методи, що повертають нову позицію в залежності від напрямку руху по полю. Також ми перевизначаємо методи __eq__ і __hash__ для порівняння позицій і використання в якості ключів для словника поля. Поле - це словник, де ключі відповідають позиції на полі, а значення - це вартість найкоротшого маршруту, що приводить в дану позицію.

Прийшов час створити клас безпосередньо для самої гри

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import queue

class Game(object):

    def __init__(self, initial_state: Cube, start: Position, end: Position):
        self.initial_state = initial_state
        self.start = start
        self.end = end
        self.map = dict()
        self.queue = queue.Queue()
        self._min_score = float('inf')

    def solve(self):
        pass

На вхід потрібно отримати початковий стан кубика, точку початку та точку кінця. Також ми зберігаємо поле, чергу для перебору шляхів і поточну мінімальну ціну шляху. Почнемо покроково розглядати наш найголовніший метод solve

1
2
self.queue.put((self.start, self.initial_state))
self.map[self.start] = self.initial_state.value

Ми додаємо в чергу пару початкової позиції та початкового стану, а на полі позначаємо вартість шляху - це значення нижньої грані в поточний момент. І поки черга не порожня, ми перебираємо усі можливі варіанти переміщення і фільтруємо для наступних кроків лише оптимальні з них.

1
2
3
4
5
while not self.queue.empty():
    pos, state = self.queue.get()
    min_score = self.map[pos]
    if pos == self.end and min_score < self._min_score:
        self._min_score = min_score

Кожен крок починаємо з отримання останнього (FIFO) елементу в черзі. Для початку робимо перевірку, чи досягнутий кінець шляху і чи вартість поточного маршруту є найменшою.

1
2
3
4
5
6
for direction in ('forward', 'right', 'backward', 'left'):
    new_pos = getattr(pos, direction)()
    move_method = f'move_{direction}'
    new_state = getattr(state, move_method)()
    new_value = min_score + new_state.value
    current_value = self.map.get(new_pos, self._min_score)

Далі перебираємо всі можливі напрямки і для кожного з них отримуємо нову координату і нове положення кубика, а також отриману вартість шляху за умови, що ми продовжимо рух в цьому напрямку.

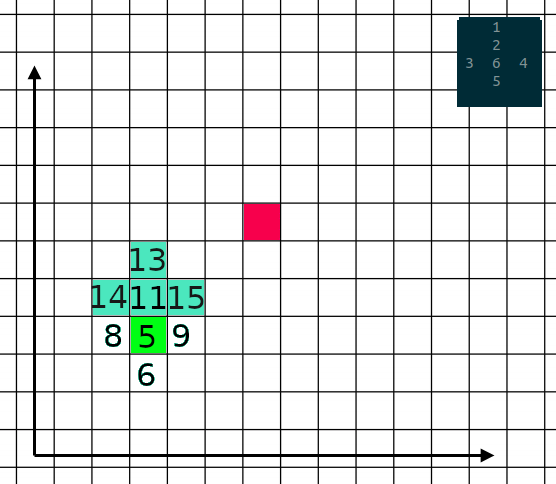
позиція після першого кроку

1
2
3
if new_value <= current_value:
    self.map[new_pos] = new_value
    self.queue.put((new_pos, new_state))

Якщо шлях оптимальний - продовжуємо рухатися ним (додаємо в чергу для наступного кроку і записуємо значення в клітинку поля). В кінці функції повертаємо результатом вартість найдешевшого маршруту return self._min_score.

Побудова шляху

Отримати вартість найдешевшого шляху - це лише одна частина. Набагато цікавіше - дізнатися сам маршрут, по якому потрібно рухатися кубику. Найочевидніший варіант - це зберігати у черзі замість пар трійку значень: (позиція; стан; послідовність кроків, яка привела в дану клітинку). Такий підхід теж дуже затратний по пам’яті, оскільки вимагає зберігання шляхів для кожної з точок поля, а їх кількість зростає поліноміально з кожним кроком, та і сама довшина шляху є лінійно зростаючою. Краще додати ще один додатковий крок, який буде рухатися з фінішної точки в зворотному напрямку по уже побудованому мінімальному шляху, а потім просто розвернути цей шлях в іншому напрямку.

Спочатку визначаємо словник, який допоможе нам створити зворотній напрямок

1
2
3
4
5
6
REVERSED_DIRECTIONS_ABBR = {
    'backward': 'F',
    'left': 'R',
    'forward': 'B',
    'right': 'L',
}

І стоворимо додаткову функцію, яка допоможе обрати мінімальний напрямок із заданої позиції

1
2
3
4
5
6
7
8
9
10
def _get_min_direction(self, pos):
    min_score = float('inf')
    min_direction = None
    for direction in ('backward', 'left', 'forward', 'right'):
        new_pos = getattr(pos, direction)()
        if self.map.get(new_pos, min_score) < min_score:
            min_score = self.map[new_pos]
            min_direction = direction

    return min_direction

Для кожної клітинки розглядаємо її сусідів і вибираємо найоптимальніший напрям. Залишилося описати саму функцію пошуку шляху.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def get_path(self):
    if self._min_score == float('inf') or not self.map:
        raise RuntimeError('No solution! '
                           'Have you solved the game already?')
    pos = self.end
    path = [f'{self.end}[{self._min_score}] DONE!']
    while pos != self.start:
        min_direction = self._get_min_direction(pos)
        pos = getattr(pos, min_direction)()
        move = self.REVERSED_DIRECTIONS_ABBR[min_direction]
        score = self.map[pos]
        path.append(f'{pos}[{score}] -> {move}')

    return reversed(path)

Працює вона описаним вище шляхом: починаючи з фінішу, рухаємося до мінімальних сусідів і додаємо “обернене” ім’я кроку до загального шляху. Досягнувши старту - повертаємо шлях у зворотному напрямку, що уже містить правильні “обернені” назви для напрямків руху. Залишилося найважливіше - запустити і перевірити алгоритм в дії:

1
2
3
4
5
6
7
8
9
10
11
12
13
cube = Cube(
    front=1,
    back=6,
    bottom=5,
    top=2,
    left=3,
    right=4,
)
start = Position(2, 2)
end = Position(5, 5)
game = Game(initial_state=cube, start=start, end=end)
print(game.solve())
print('\n'.join(game.get_path()))

На моєму ноутбуці результат виглядає так:

1
2
3
4
5
6
7
8
22
(2, 2)[5] -> R
(3, 2)[9] -> R
(4, 2)[11] -> F
(4, 3)[16] -> F
(4, 4)[18] -> F
(4, 5)[19] -> R
(5, 5)[22] DONE!

Двічі рухаємося вправо, тричі вгору і після останнього повороту вправо досягаємо фінішу за 22 одиниці. Результат може відрізнятися, якщо змінити порядок вибору напрямків ('forward', 'right', 'backward', 'left'), але мінімальна вартість буде завджи така ж сама.

Що далі?

Отож, ми створили представлення кубика та поля в коді для розв’язанн задачі з пошуку мінімального шляху. Існує припущення, що дану задачу можна вирішити алгоритмом, що працює за лінійний час. Ми спробуємо довести це в наступних частинах цієї статті. Також створимо набагато кращу візуалізацію цього процесу і проведемо детальний аналіз затрат по часу та пам’яті для кожного з розглянутих рішень. Сподіваюсь, щось з цього було корисно, до зустрічі ;)

Ресурси